• 완전 탐색 (Exhaustive Search) 이란?
컴퓨터의 빠른 연산 능력을 활용하여 가능한 모든 경우의 수를 일일히 대입하여 해를 찾는 방법.
무차별 대입하여 탐색한다는 의미로써 Brute force search 로 명칭하기도 한다.
이는 효율을 중시하기보단 정확성을 중시하는 문제 해결 기법으로써
입력의 수에 따라 시간복잡도가 기하급수적으로 증가하기 때문에
그 수가 적은 문제에 활용하기 적합하다.
• 완전 탐색의 종류
1. Brute Force
단순히 반복문이나 조건문을 다중으로 사용하여 처음부터 끝까지 모든 경우의 수를 구하는 기법.
이는 주로 기초적인 문제나 전체 문제 풀이의 일부분에 활용된다.
예시로 배열의 요소의 수 만큼의 중첩 for 문을 사용하여 요소의 모든 순열을 찾을 수 있다.
int[] arr = { 1, 2, 3 };
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
for (int k = 0; k < arr.length; k++) {
if (i == j || j == k || k == i)
continue;
System.out.println(arr[i] + "" + arr[j] + "" + arr[k]);
}
}
}이는 입력의 수에 따라 심각한 비효율을 초래할 여지가 있어 적절한 상황에 사용하도록 유의해야 한다.
2. 재귀 (Recursive)
자기 자신을 호출하는 함수, 즉 재귀 함수를 활용하여 문제의 해를 구하는 기법.
재귀 함수란 특정 작업이 일정한 패턴을 가지고 반복된다면, 해당 패턴의 한 부분을 수행하는 함수를 생성하고
그 함수가 다시 자기 자신을 호출하여 반복 실행하는 것을 말한다.
이때 조건없이 재귀 함수를 계속 호출할 시 무한으로 반복되므로 재귀 함수를 탈출하기 위한 탈출 조건이 필요하고
이러한 탈출 조건을 지정하기 위해선 현재 함수의 상태를 저장하는 변수를 생성할 필요가 있다.
3. 순열 (Permutation)
서로 다른 n개의 요소의 임의의 수열이 주어졌을 때 특정한 순서로 r 개를 선택 혹은 나열하는 경우의 수이며
그러한 순서가 문제의 해와 관련해 의미가 있는 경우 순열 문제라 할 수 있다.
아래와 같이 재귀 함수로 구현하거나
C++ 은 next_permutation(), 파이썬은 itertools.permutation 으로 구현 가능하다.
static int n = 3;
static int r = 3;
static int[] arr = { 1, 2, 3 };
static int[] result = new int[r];
static boolean[] visit = new boolean[n];
public static void main(String[] args) {
permutation(0);
}
private static void permutation(int idx) {
if (idx == r) {
System.out.println(Arrays.toString(result));
return;
}
for (int i = 0; i < n; i++) {
if (!visit[i]) {
result[idx] = arr[i];
visit[i] = true;
permutation(idx + 1);
visit[i] = false;
}
}
}
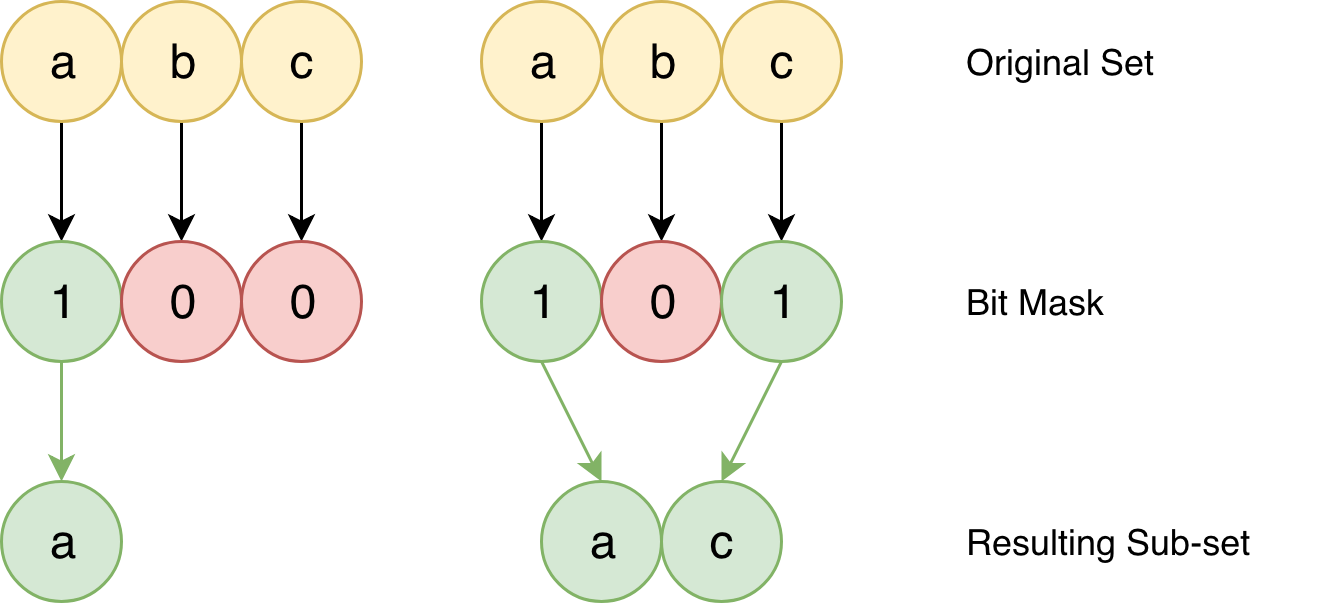
4. 비트 마스크 (Bit Mask)
2진수를 사용하는 컴퓨터 연산 방식을 활용하여, 정수의 2진수 표현을 자료구조로 쓰는 기법으로
비트는 0 또는 1 (false or true) 만의 값을 가지며 and, or, xor, not, shift 연산으로 제어한다.
이는 문제 중 특정 경우의 수가 두 가지 선택으로 구성되는 경우에 유용히 사용 가능한데,
예시로 원소가 n개인 집합의 모든 부분 집합을 구할 때
집합의 각 원소가 해당 부분 집합에 포함되거나 포함되지 않는 2 가지 경우가 존재하므로
아래와 같이 n자리 2진수를 활용하여 문제를 풀이할 수 있다.
5. DFS / BFS
문제 중 그래프 자료구조에서 모든 정점을 탐색해야 하는 경우 사용된다.
자세한 내용은 아래의 포스팅으로 대체한다.
[알고리즘] 그래프 순회 (Graph Traversal)
• 그래프 순회 (Graph Traversal) 란? 정점(node) 과 그 정점을 연결하는 간선(edge) 으로 이루어진 자료구조를 그래프(graph) 라 한다. 그래프의 하나의 정점으로부터 시작하여 모든 정점을 한 번씩 방문
graycode.tistory.com
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] 그래프 순회 (Graph Traversal) (0) | 2022.05.16 |
|---|---|
| [알고리즘] 동적 계획법 (Dynamic Programming) (0) | 2022.05.06 |
| [알고리즘] 탐욕법 (Greedy Algorithm) (0) | 2022.05.03 |



댓글